再經過前面兩節的介紹之後，想必讀者一定都有了基礎的概念，最後這一小節，我將舉出四個例子，讓大家能更具體的瞭解如何使用這個計算方法，也建議讀者們可以先把答案遮起來，自己算算看！最後再帶入第一節所要講的證明，畫下一個完美的句點。
範例一
$\Large\int{\ln xdx}$
(讀者可以自己試試看一步一步分部積分，再來比較此法的速度、以及計算難易度)
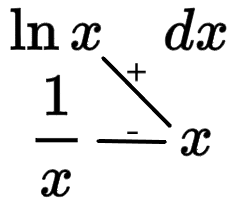所以為$\Large x\ln x- \int 1dx= x\ln x- x+c$
範例二
$\Large\int{e^{3x}\sin 2xdx}$
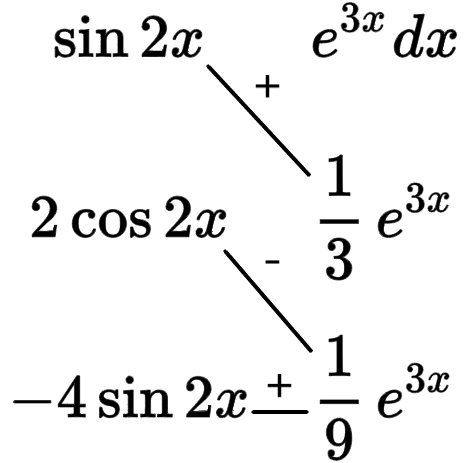
所以$\Large\int e^{3x}\sin 2xdx=\frac{1}{3} e^{3x}\sin2x-\frac{2}{9} e^{3x}\cos2x-\int\frac{4}{9}e^{3x}\sin 2xdx$
$\Large\Rightarrow\frac{13}{9}\int e^{3x}\sin 2xdx=\frac{1}{3} e^{3x}\sin2x-\frac{2}{9} e^{3x}\cos2x+c$
$\Large\Rightarrow\int e^{3x}\sin 2xdx=\frac{3}{13}e^{3x}\sin2x-\frac{2}{13}e^{3x}\cos2x+c$
大家積出來之後，可以微分回去，驗算看看對不對
範例三
$\Large\int_{0}^{1}{x2^xdx}$
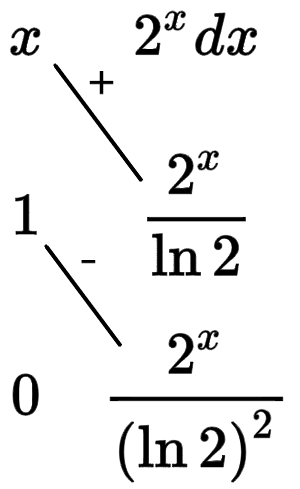
$\Large\int_{0}^{1}{x2^xdx}=\left(x\cdot \frac{2^{x}}{\ln 2}-\frac{2^{x}}{\left(\ln 2\right)^{2}}\right) \Bigg| _{0}^{1}$
範例四
$\Large\int{\sin^{-1} xdx}$
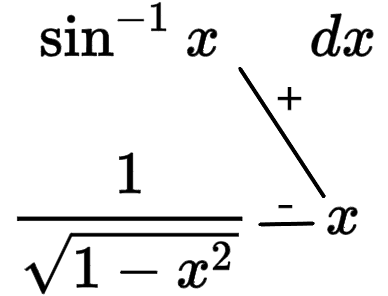請看附錄<反三角函數的微分>
所以$\Large\int{\sin^{-1} xdx}=x\sin^{-1} xdx-\int{\frac{xdx}{\sqrt{1-x^2} } }$
其中$\Large\int{\frac{xdx}{\sqrt{1-x^2} } }=\int{\frac{-udu}{u} }$
(令 $\Large u={\sqrt{1-x^2}}\quad \Rightarrow u^2=1-x^2\Rightarrow 2udu=-2xdx$)
故$\Large\int{\sin^{-1} xdx}=x\sin^{-1} xdx+\sqrt{1-x^2}+c$
心得：
由此，我們可以觀察出三大類情況：
1. 微到 0 為止，如範例三
2. 微到可以積的項，如範例一、範例四
3. 微出自己本身，如範例二
當然也有第四種情況是最後是積不出來的(仍留下積分項)，但經過I.B.P後有降階的效果(降到不能再積為止)
通常會把可以微到0的放左邊，如多項式部分
好積的，如$e^x$、$\sin x$、$\cos x$放右邊
請看附錄<反三角函數的微分>
請看附錄<快速積分法第一節跳過的證明>
