題號:397
科目:資料結構與演算法(A)
本試卷共20題選擇題,作答於答案卡。每題答對5分,不答零分,答錯倒扣2.5分。
$I.$ When CAN the worst case of Quicksort occur? _____(1)_____
$\small \quad C_{1}:$ Quick Sort where leftmost (or rightmost) element is always chosen as pivot
$\small \quad C_{2}:$ leftmost element is chosen as pivot and array is already sorted in SAME order
$\small \quad C_{3}:$ leftmost element is chosen as pivot and array is already sorted in REVERSE order
$$\small (A) \, C_{1} \quad (B) \, C_{2} \quad (C) \, C_{1} \, \text{and} \, C_{2} \quad (D) \, C_{2} \, \text{and} \, C_{3}$$
參考解答:(1) D

$II.$ A typical dynamic programming example is the snake sequence. Given a grid of numbers, find maximum length snake sequence and print it. A snake sequence is made up of adjacent numbers in the grid such that for each number, the number on the right or the number below it is $\small +1$ or $\small -1$ its value. For example, if you are at location $\small (x, \, y)$ in the grid, you can either move right $\small i.e. (x+1, \, y)$ if that number is $\small \pm 1$ or move down $\small i.e. (x, \, y+1)$ if that number is $\small \pm 1$. The length of a snake sequence is defined as the number of moves. Given the following grid (A matrix with $\small M$ rows and $\small N$ columns),
$\small \qquad \qquad \begin{aligned} &9, \, 6, \, 5, \, 2 \\ & 8, \, 7, \, 6, \, 5 \\ &7, \, 3, \, 1, \, 6 \\ &1, \, 1, \, 1, \, 7 \end{aligned}$
$\small (a)$ The maximum LENGTH of snake sequence is _____(2)_____
$$\small (A) \, 6 \quad (B) \, 7 \quad (C) \, 5 \quad (D) \, 4$$
$\small (b)$ Time complexity of above solution is _____(3)_____
$$\small (A) \, O(M \times N) \quad (B) \, O(M^2) \quad (C) \, O(N^2) \quad (D) \, O(M)$$
$\small (c)$ The last number of the maximum-length snake sequence is _____(4)_____
$$\small (A) \, 9(0, \, 0) \quad (B) \, 6(3, \, 2) \quad (C) \, 7(3, \, 3) \quad (D) \, 1(2, \, 3) \quad (E) \, 7(0, \, 2)$$
$\small (d)$ The third number of the maximum-length snake sequence is _____(5)_____
$$\small (A) \, 7(1, \, 1) \quad (B) \, 7(0, \, 2) \quad (C) \, 3(1, \, 2) \quad (D) \, 6(2, \, 1) \quad (E) \, 8(0, \, 1)$$
參考解答:(2) A (3) A (4) C (5) A

$III.$ For questions with sequences, we constantly split the problem into a number of sub-problems that are smaller instances of the same problem, and we try to solve the smaller problem recursively. We called this type of algorithm _____(6)_____
$$\small (A) \, \text{Dynamic programming} \quad (B) \, \text{Divide and conquer} \quad (C) \, \text{Greedy algorithms} \quad (D) \, \text{Quicksort}$$
參考解答:(6) B

$IV.$ There is a large enough array $\small A$ with indices $\small p$ and $\small q$ which are initialized by $\small 0$, and functions $\small f(x)$ and $\small g()$ are defined as follows. Array $\small A$ and indices $\small p$ and $\small q$ can only be accessed in the functions $\small f(x)$ and $\small g()$.
$\small \qquad \qquad \begin{aligned} &f(x) \\ &\cdot \, p \leftarrow p + 1 \\ &\cdot \, A[p] \leftarrow x \\ &g() \\ &\cdot \, x \leftarrow A[p] \\ &\cdot \, p \leftarrow p – 1 \\ &\cdot \, \text{return} x \end{aligned}$
$\small (a)$ Which data structure is operated by those functions? _____(7)_____
$$\small (A) \, \text{Queue} \quad (B) \, \text{Stack} \quad (C) \, \text{Hash} \quad (D) \, \text{Heap}$$
$\small (b)$ If functions $\small f(x)$ and $\small g()$ are changed as following:
$\small \qquad \qquad \begin{aligned} &f(x) \\ &\cdot \, A[q] \leftarrow x \\ &\cdot \, q \leftarrow q + 1 \\ &g() \\ &\cdot \, x \leftarrow A[p] \\ &\cdot \, p \leftarrow p + 1 \\ &\cdot \, \text{return} x \end{aligned}$
Which data structure is operated by those functions? _____(8)_____
$$\small (A) \, \text{Queue} \quad (B) \, \text{Stack} \quad (C) \, \text{Hash} \quad (D) \, \text{Heap}$$
參考解答:(7) B (8) A



參考解答:
(a) C
(b) A

參考解答:
(a) C
(b) D

參考解答:B
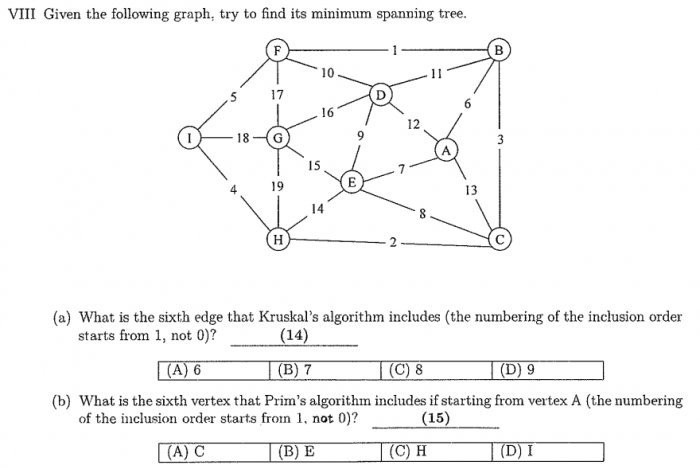
參考解答:
(a) B
(b) B
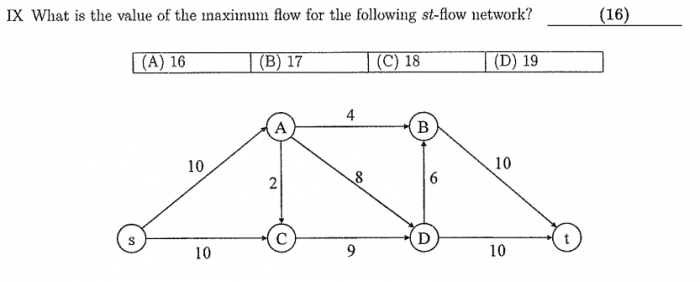
參考解答:D

參考解答:B

參考解答:D

參考解答:A
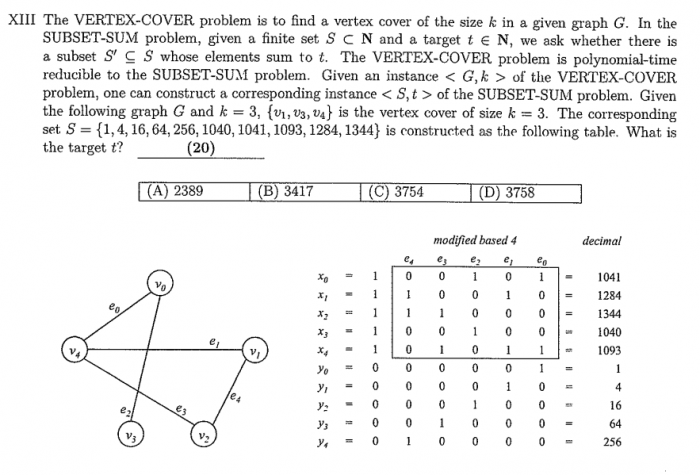
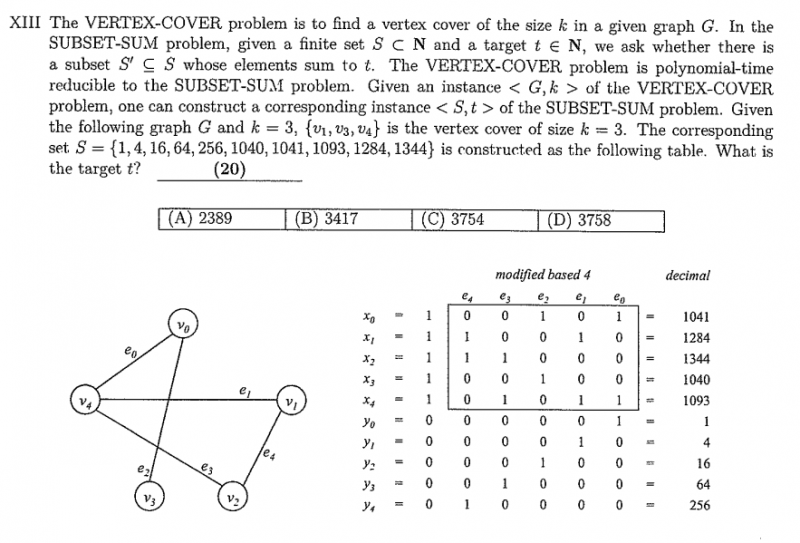
參考解答:C

第6題方便詳解嗎 我把16進制轉成10進制後各求出餘數 但解出來的答案對不上
周辰 你好:
第六題(a)答案已由B更正為C,謝謝你。
如果還有發現其他題怪怪的再跟我們反應唷!
想請問第7題,我算time complexity分別是f1(n):n、g1(n):n、f2(n):1、g2(n):1,這樣答案會是B、D,但您的答案是B,不知道是我哪裡算錯了呢? 謝謝!
PING 你好:
第七題的g2(n)的complexity應該是O(n),因為雖然我們加了一個tail pointer但是當我們刪除的時候你還是要知道倒數第二個element是誰然後把它的next指向nil。希望這樣有回答到,加油~
請問最後一題怎算的 因為我算出來的是3754
您好:
最後一題的答案是3754沒錯,已將答案更正為C,謝謝你。
可以問一下最後一題是怎麼算的嗎?
有點看不太懂題目
ptt的文章討論看完也不太理解…
https://www-geeksforgeeks-org.translate.goog/subset-sum-is-np-complete
但他這題還額外加了 3 個 1024 來說明取 3 個點這件事
想請問一下第11題,看的出題目跟狀態有限機有關係
但是他的表格讓我有看沒有懂
想求個詳解?
您好 我也想請問11題的表格到底代表什麼意思
再麻煩大大幫忙
感謝~
您好 , 我也想請教11題的詳解(表格代表的意思)
再麻煩版主幫忙了
感謝Orz
第15題 我追出來的順序是abfchi 第六個點是I 想問一下版主是怎麼追的?
+1 我也是這順序
請問有其他年份的台大資工解答嗎
想請問第2題的最大長度為何不是7?
經過7個頂點{9->8->7->6->5->6->7}需要|V|-1個邊,所以應該是7-1=6個邊長