什麼是漸進符號
我們通常會用函數來表示演算法的時間及空間複雜度,而漸進符號其實就只是要表達這個函數簡化後的形式,或者也可以說,讓我們知道這個函數的“等級”。
有了演算法複雜度等級之後,我們可以更簡單的與其他演算法進行比較,從中找出最有效率的演算法。
漸進符號有哪些
1. $O$ – notation (Big-oh)
2. $\Omega$ – notation (Big-omega)
3. $\Theta $ – notation (Big-theta)
4. $o$ – notation (Little-oh)
5. $\omega $ – notation (Little-omega)
1-3 這三個是最常使用的漸進符號,尤其是第一個 Big-Oh, 4-5 則幾乎不會用到。下面我會介紹這五個漸進符號的定義及例子。
Big-oh
假設 $f$, $g$ 為兩個函數,則定義如下
$$O(g(n)) = { f(n): \exists c > 0, \ n_{0} > 0 \, \ s.t. \, 0 \leq f(n) \leq c \, g(n), \ \forall n \geq n_{0} } $$
從定義可以看出 $O(g(n))$ 是一個專門搜集 $f(n)$ 這種元素的集合,也就是說若 $ f(n) \in O(g(n))$ 則代表存在正整數 $c, n_{0}$ 對於所有 $n \geq n_{0}$ 均滿足 $\leq f(n) \leq c \, g(n)$。如果覺得太抽象的話我們可以看下面這個例子:
例:假設 $f(n) = 5n + 5$ 且 $g(n) = n$,則我們取 $c = 6$ 及 $n_{0} = 5$ 來驗證看是否滿足定義:
1. $c, n_{0}$ 皆為正整數
2. $n = 5$ 時代入得 $f(5) = 30, \, 6 \times g(5) = 30$ 符合 $0 \leq f(n) \leq c \, g(n)$,繼續代 $n = 6, \, n = 7, \, \cdots$ 你會發現都將符合定義 (可參考下圖)
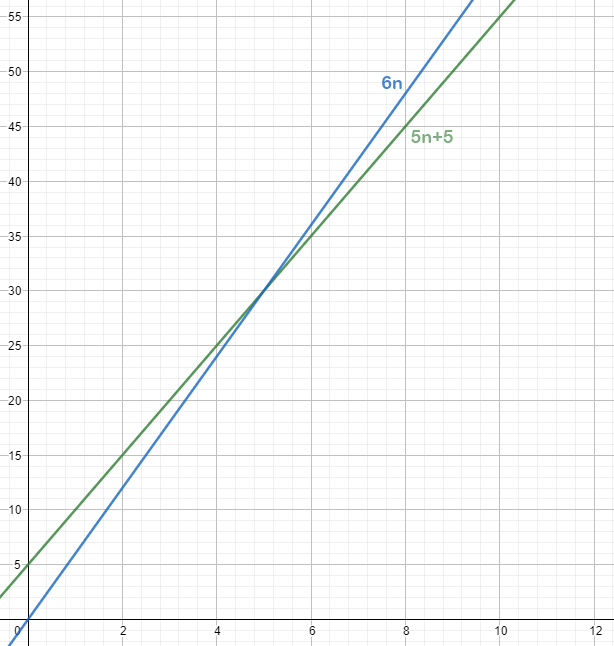
經過上述驗證後,可以得到 $5n + 5 \in O(n)$,或 $5n + 5 = O(n) $ 。
在漸進符號這個主題裡 $\in$ 也可以記作 $=$,很多演算法書籍也都會直接用$=$,並不是寫錯了!
看到這裡,不知道你有沒有發現到,其實 $O(g(n))$ 就是要搜集那些成長速率比自己小或者與自己相差常數倍的函數,也是我們常常用來表示一個演算法複雜度上界(upper bound)的符號。
當討論一個演算法複雜度時,我們對它在最壞情況(worst case)的表現最有興趣,這也是為什麼 $O(\cdot)$ 比其它漸進符號更常被使用到。
在真正討論演算法的複雜度時,我們最常用的就是 Big-Oh,若對其他複雜度嚴謹的定義有興趣的讀者,可以參考演算法的書籍或維基百科。

<<Introduction to Algorithms>> 俗稱楓葉書或是 CLRS(作者名)由 Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein 撰寫,是演算法的聖經書。聽說每個軟體工程師的包包裡面都會有一本。