必看！超快積分法，必會積分技巧，超高計算速度，再也不會計算凸槌(2)

上一節我們導出了
$$\Large\int{udv}=uv-\left(u’v_{1}-\int{v_{1}u^{\prime\prime}dx}\right)$$
$$\Large=uv-u’v_{1}+\int{v_{1}u^{\prime\prime}dx}\qquad(3)$$
其中的$$\Large\int{v_{1}u^{\prime\prime}dx}=\int{u^{\prime\prime}v_{1}dx}$$
令
$\large u_{new} =u^{\prime\prime}\quad\qquad du_{new} =u^{(3)}dx$
$\large dv_{new} =v_{1}dx\qquad v_{new} =v_{2}$
得
$$\Large\int{u^{\prime\prime}v_{1}dx}=u^{\prime\prime}v_{2}-\int{v_{2}}u^{(3)}dx$$
帶回原式
$$\Large\int{udv}=uv-u’v_{1}+\int{v_{1}u^{\prime\prime}dx}$$
$$\Large=uv-u’v_{1}+u^{\prime\prime}v_{2}-\int{v_{2}}u^{(3)}dx\qquad(4)$$
其中的
$$\Large\int{v_{2}u^{(3)}}dx=\int{u^{(3)}v_{2}}dx$$
令
$\large u_{new} =u^{(3)}\quad\qquad du_{new} =u^{(4)}dx$
$\large dv_{new} =v_{2}dx\qquad v_{new} =v_{3}$
得
$$\Large\int{u^{(3)}v_{2}dx}=u^{(3)}v_{3}-\int{v_{3}}u^{(4)}dx$$
帶回原式
$$\Large\int{udv}=uv-u’v_{1}+u^{\prime\prime}v_{2}-\int{v_{2}}u^{(3)}dx$$
$$\Large=uv-u’v_{1}+u^{\prime\prime}v_{2}-\left(u^{(3)}v_{3}-\int{v_{3}}u^{(4)}dx\right)$$
$$\Large=uv-u’v_{1}+u^{\prime\prime}v_{2}-u^{(3)}v_{3}+\int{v_{3}}u^{(4)}dx\qquad(5)$$

可以發現我們已經推出一個規則，還可用圖表的方式幫助我們記憶、運算

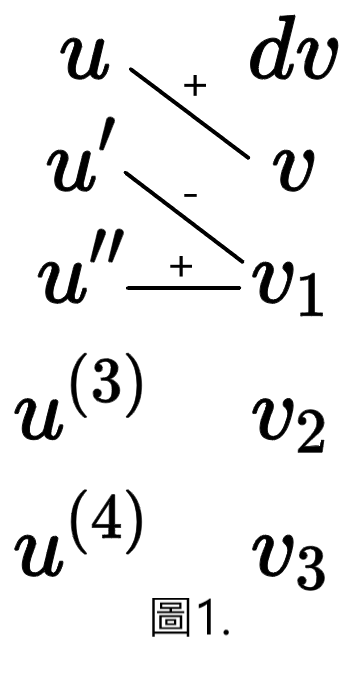$\qquad$ 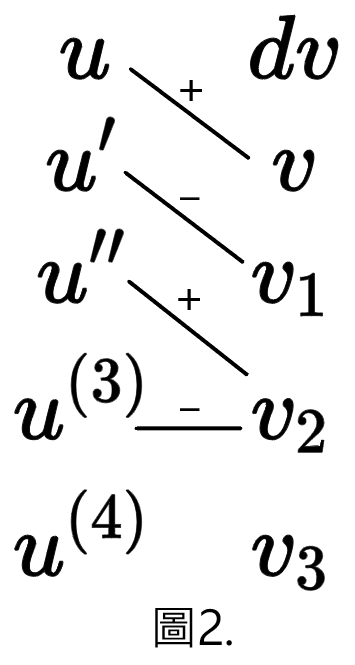$\qquad$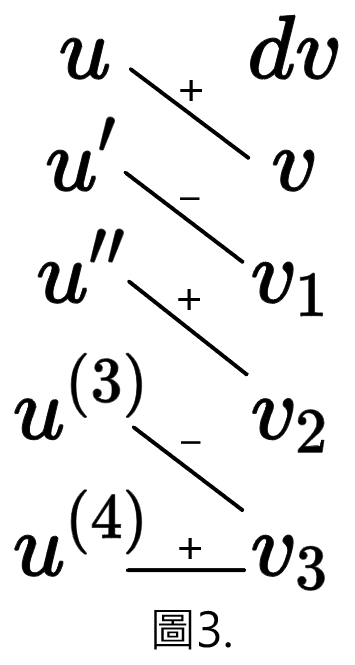

圖1.、圖2.、圖3.，分別對應到 式(3)、式(4)、式(5)
由於 I.B.P 不論如何一定會拆出一個積分，此積分項即最後一項 (水平線的項)
故此最後一項要補上 $\large\int{(\quad)}dx$

注意事項：

小細節別忘記！以免要用時又不知道該如何用！

1. 第1條斜線為正
2. 每畫一條線就要變號一次
3. 左邊放 $u$ 右邊放 $dv$ ，左邊一直微，右邊一直積
4. 最後一項(水平項)記得補上 $\large\int{(\quad)}dx$

請接續看 <必會積分技巧之三>