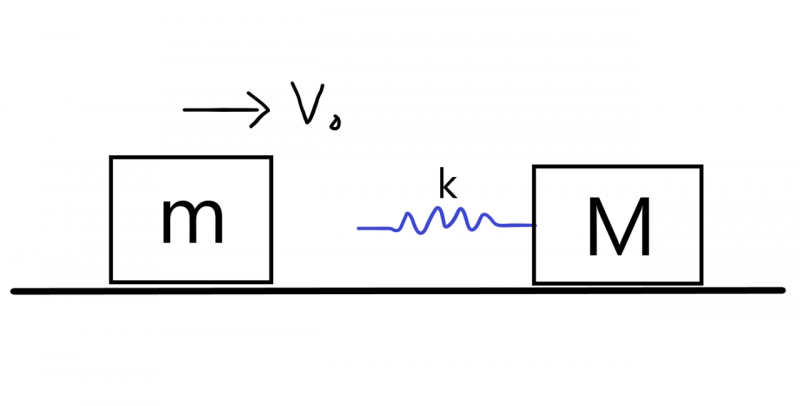
在高中物理碰撞這個單元裡面,常會碰到一個經典的題目,題目如下圖
高中老師看到這個題目通常都會直接叫你把答案背起來,那想必一定會有不少同學很好奇這題到底要怎麼解,Grandy這邊提供兩種解法,一種是用python跑模擬,程式百分之百是自己寫的,沒有用到任何library,這種方法高中生、甚至國中生都可以理解;第二種方法是使用微分方程式解出運動方程,但這需要較高的數學知識,可能需要到大一、大二的程度才能理解,但還是很推薦高中生們欣賞看看。
我們先來分析兩物體的受力情況:
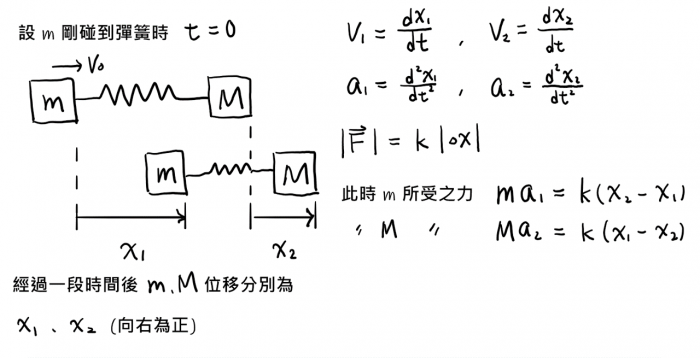
如圖所示,我們令 $m$ 剛碰到彈簧時(碰撞剛發生時),$t=0$,並且令向右為正。
經過一段時間之後,兩剛體皆向右移動一段距離,我們令 $m$ 的位移為 $x_1$,$M$ 的位移為 $x_2$
$m$ 的速度 $v_1$,為$x_1$的一次微分,如果$x_1$的一次微分微出來是負的,就代表此時速度向左;$x_1$ 的一次微分微出來是正的,就代表此時速度向右。同樣的,若二次微分微出來是負的,代表加速度向左;二次微分微出來是正的,就代表此時速度向右。$M$ 也是如此道理,就不再贅述。
接著,彈簧的恢復力為 $F=k\left|\Delta x \right|$,這邊方向就需要大家自己判斷,因為 $a_1$ 應該是負的(此時 $m$ 受彈簧力向左) 所以等號右邊就應該要一樣是負的值,$\left|x_1-x_2 \right|$ 就是彈簧縮短的量,那我們要取負的,所以就得到$ma_1=x_2-x_1$ (因為碰撞剛發生的時候可以想見 $x_1>x_2$ ),相同道理,$M$ 的受力分析就交由大家自己練習。
高中的話到這裡就沒辦法繼續解下去了,所以我們先用程式來模擬看看,以下為完整程式碼:
#作者: Grandy 日期:2021/8/3
#雙振子碰撞時間模擬
dt=0.0000001
m=5
M=10
Vm,VM=50,0 #初速
am,aM=0,0 #初加速度
XM,Xm=0,0
k=8
i=0 #記數,算經過多少time=i*t
while (XM-Xm)<=0:
am=k*(XM-Xm)/m
aM=k*(Xm-XM)/M
Vm=Vm+am*dt
VM=VM+aM*dt
Xm=Xm+Vm*dt
XM=XM+VM*dt
i+=1
t=i*dt
print(t)
只要我們把時間取得夠小,那麼在每一段時間間隔內,都可以視作等狀態的(等速度、等加速度、等外力),所以先把 dt 取 0.1 微秒,因為是等速度的關係,所以這段時間內前進的位移就是”速度X時間間隔”,速度變化量就是”加速度X時間”。所以我們先把前面推出的加速度代入,推出下一時間間隔的速度,就可以推出下一時間間隔的位移;有了新的位移,就得到新的加速度,再推出新的速度、位移,如此循環,就可以模擬出兩物體的運動狀態。又每做一次while loop,模擬世界中就經過了0.1微秒,所以只要統計做了幾次whlie迴圈,就可以知道碰撞歷時多久了!
我們要知道什麼時候碰撞停止,這樣才有辦法給whlie條件。很直覺的就是如果仍有接觸,那我們就說碰撞還沒停止,那什麼時候沒有接觸了,就是碰撞結束的時候。所以當 $x_1>x_2$ 時,很明顯 $m$ 還跟彈簧有接觸,那當 $x_1=x_2$ 時,應該就是碰撞結束的時候了。我們再換另一個角度想,這是一個彈性碰撞,彈性碰撞就是內動能轉成位能,位能再轉回動能,那麼位能再度歸零時,應該就是碰撞結束的時候了,所以 $x_1=x_2$ 時,彈簧的位能等於零,碰撞結束。
這邊要注意的是,雖然當 $x_1=x_2$ 時,碰撞結束,但若while條件裡只寫 $x_M<x_m$ 的話,會跑不進while而直接輸出0,因為一開始 $x_M=x_m=0$。
讀者們也可以試試看改動前面幾行的參數,就發現這的確是個成功的程式,可以幫我們模擬出雙振子的碰撞時間為理論值:雙振子週期的一半,即:$\frac{1}{2} \times 2\pi\sqrt{\frac{\mu }{k}}$
下一節,我們將帶大家看看如何用物理的角度,解微分方程,得到答案。
完整影片講解如下:https://youtu.be/jBShUtxXM60