在這系列文章中，我們已經探討了各種微分方程式的類型和解法。這篇文章將進入更為複雜的領域：偏微分方程式（Partial Differential Equations，簡稱PDEs）。
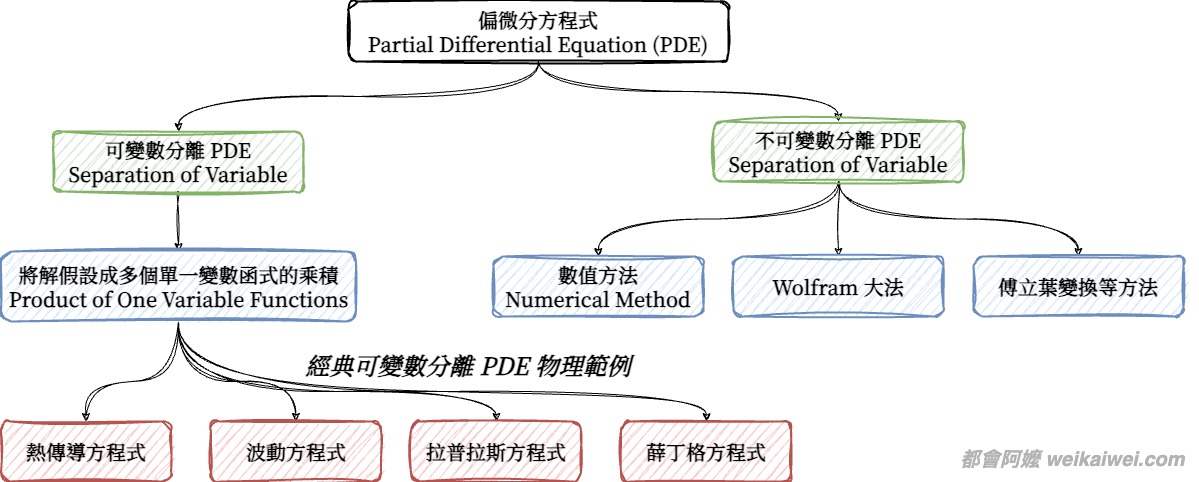
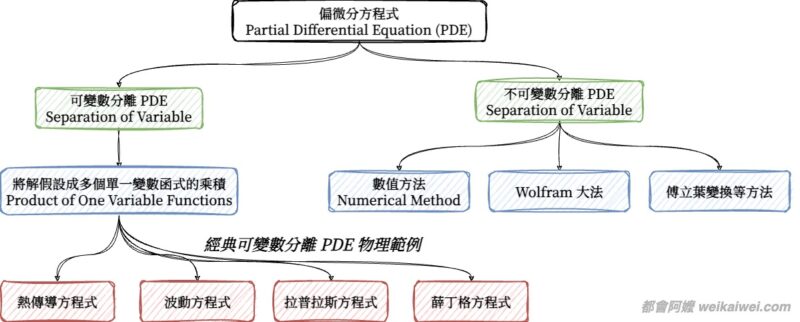
偏微分方程式涉及多個自變數（independent variables 的方程式，這與我們之前討論的常微分方程式（ODEs）有所不同。偏微分方程式在描述例如熱傳導（heat conduction）、波動傳播（wave propagation）、流體動力學（fluid dynamics）等現象時非常有用。
在這篇文章中，我們將特別集中討論可分離偏微分方程式（Separable PDEs)，也就是「方程式解」可以拆成多個「簡單」函數相乘的情況。 這是解決許多物理和工程問題的關鍵。後續會看到非常多著名的範例都是可分離偏微分方程式。
然而心裡一定要有一個蓋念，絕大部分現實世界、物理世界真實的方程式都不是可分離的、都不是容易解的，所以數值方法（numerical methods) 一定也要會，或至少也要會用 WolframAlpha （笑）。
不可分離的偏微分方程式
首先，讓我們快速帶過不可分離的偏微分方程式（Non-separable PDEs）。這類方程式的特點是，它們不能簡單地分解為單一自變數的方程式。這代表整體解的結構比可分離的情況更為複雜。
例如，許多非線性偏微分方程式都屬於這個範疇，並且常常需要使用數值方法或者專門的解析技巧來找到解答，如傅立葉變換（Fourier Transform）、變分法（Variational Methods）等等。
可分離偏微分方程式 (Separable Partial Differential Equation)
相對於不可分離的偏微分方程式，可分離偏微分方程式提供了一個更為直觀的解法途徑。在某些條件下，這些方程式可以通過假設解為變數分離形式（即解可以寫成自變數乘積的形式）來簡化。這種方法允許我們將一個複雜的多變數問題分解為幾個較簡單的單變數問題，每個問題都可以獨立解決。
在下一篇文章，我們會探討以下幾個經典的偏微分方程式：(1) 熱方程式 Heat Equation（2）波動方程式 Wave Equation（3） 拉普拉斯方程式 Laplace Equation，這裡先大略提一下這些方程式長什麼樣子：
熱方程式、波動方程式、拉普拉斯方程式
- 熱方程式（Heat Equation）:
$$ \frac{\partial u}{\partial t} = \alpha \frac{\partial^2 u}{\partial x^2} $$
熱方程式描述了如何通過熱傳導過程中的擴散作用來傳播熱量。它是解釋物體如何隨時間和空間變化加熱和冷卻的基礎。 - 波動方程式（Wave Equation）:
$$ \frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partial x^2} $$
波動方程式用於描述聲波、光波等波動的傳播。這個方程式幫助我們理解波動如何在不同介質中以一定速度傳播。 - 拉普拉斯方程式（Laplace Equation）:
$$
\nabla^2 u = \frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} = 0
$$
拉普拉斯方程式是一種描述在沒有外部影響時，系統達到穩態的方程。它廣泛應用於電磁學、流體力學及其他多個領域。
薛丁格方程式 （隱藏版）
對於有量子力學（Quantum Mechanics）知識的讀者，一個經典的可分離偏微分方程式是薛丁格方程式。薛丁格方程式是描述量子系統中粒子如何隨時間變化的基本方程式。這個方程式在物理教科書中通常以以下形式呈現：
時間依賴的薛丁格方程式 （Time-Dependent Schrödinger Equation）
時間依賴的薛丁格方程式描述了粒子的波函數 $\Psi(x, t)$ 隨時間的變化，它的公式如下：
$$
i\hbar \frac{\partial \Psi}{\partial t} = -\frac{\hbar^2}{2m} \frac{\partial^2 \Psi}{\partial x^2} + V(x, t) \Psi
$$
這裡，$i$ 是虛數單位（imaginary unit），$\hbar$ 是約化普朗克常數（reduced Planck’s constant），$m$ 是粒子質量（particle mass），$V(x, t)$ 是勢能（potential energy），$\Psi(x, t)$ 是波函數（wave function）。
薛丁格方程式 – 分離變數法
標準的解法是分離變數，其中將波函數 $\Psi(x, t)$ 表示為空間部分和時間部分的乘積：
$$
\Psi(x, t) = \psi(x) \phi(t)
$$
在這種表示法中，$\psi(x)$ 是空間部分的波函數，而 $\phi(t)$ 是時間部分的波函數，將 $\psi(x) \phi(t)$帶回原式後經過一翻推導，原本的偏微分方程可以被分解為兩個獨立的方程式（請容許我跳過這段推導，這部分很容易找到參考資料，而且也不難，大家可以練習看看）：
- 時間部分的方程式:
$$
\frac{d \phi(t)}{dt} = -\frac{iE}{\hbar} \phi(t)
$$
其解為：
$$
\phi(t) = e^{-iEt/\hbar}
$$ - 空間部分的方程式:
$$
-\frac{\hbar^2}{2m} \frac{d^2 \psi(x)}{dx^2} + V(x) \psi(x) = E \psi(x)
$$
這是一個時間獨立的薛丁格方程式，需要根據具體的勢能 $V(x)$ 來解。
下一篇文章，將講解熱方程式、波動方程式、拉普拉斯方程式。
