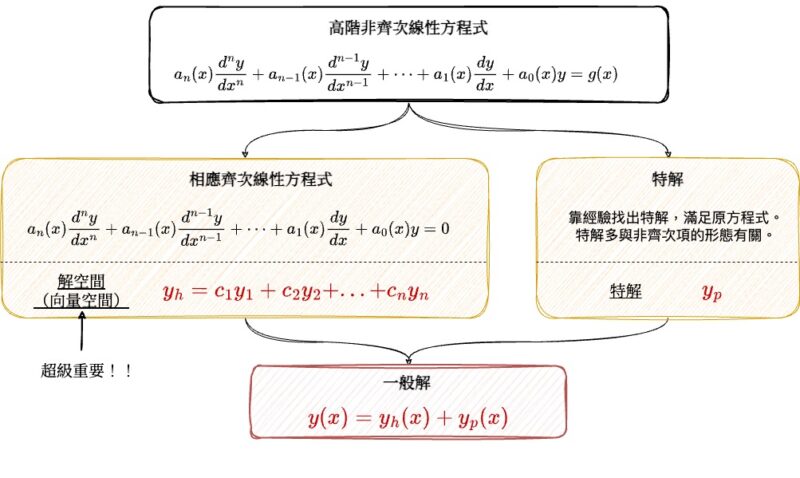
非齊次線性微分方程 在科學和工程領域中是解決許多動態系統問題的關鍵。本文將探討非齊次線性微分方程的三個基本組成部分:(1)相應的齊次微分方程、(2)特解,以及 (3)一般解。
通過理論的闡述和實際物理例子的應用,我們將深入理解這些方程的求解過程。
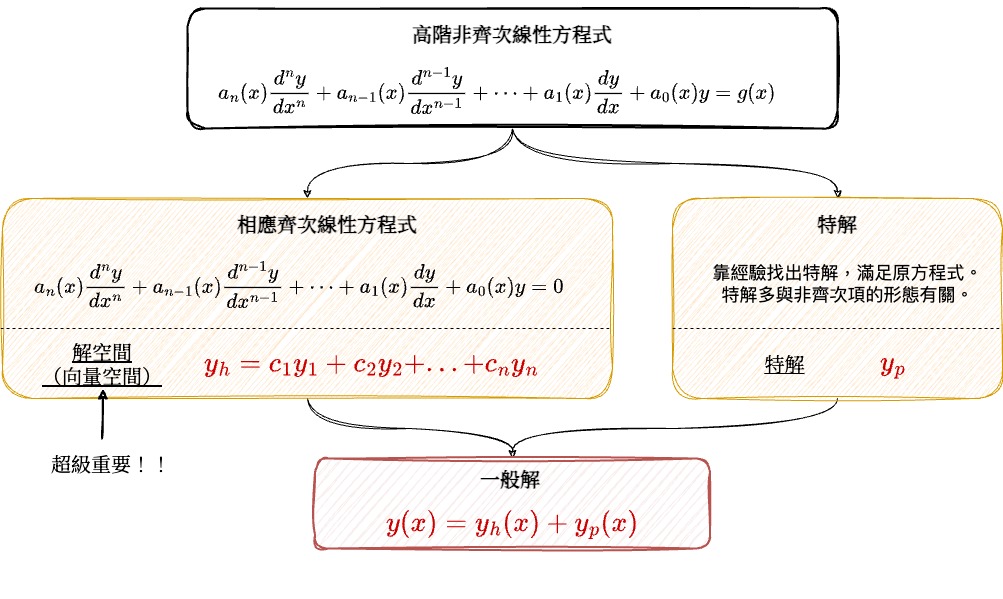
1. 相應的齊次微分方程(Associated Homogeneous Differential Equation)
非齊次線性微分方程的一般形式為:
$$a_n(x) y^{(n)}(x) + a_{n-1}(x) y^{(n-1)}(x) + \cdots + a_1(x) y'(x) + a_0(x) y = g(x)$$
其中 $y^{(n)}(x)$ 表示 $y$ 的第 $n$ 階導數,$a_i(x)$ 是 $x$ 的函數,並且 $g(x)$ 是非齊次項。相應的齊次微分方程由將非齊次項設為零得到:
$$a_n(x) y^{(n)}(x) + a_{n-1}(x) y^{(n-1)}(x) + \cdots + a_1(x) y'(x) + a_0(x) y = 0$$
求解這個齊次方程涉及找到所有使得上述等式成立的函數 $y_1, y_2, …, y_k$。這些函數形成了解空間的一組基底,從而任何解 $y_h$ 可以表示為這些基底函數的線性組合:
$$y_h = c_1y_1(x) + c_2y_2(x) + … + c_ny_n(x)$$
解這些方程的方法可能包括求解特徵方程式,該方法特別適用於常係數微分方程。
特徵方程式 (Characteristic Equation):利用指數函數的性質求解對應的特徵方程找到齊次解:
$$ r^n + a_{n-1} r^{n-1} + \cdots + a_1 r + a_0 = 0 $$
超級重要! 爲什麼要做線性組合?為什麼會形成解空間?
線性齊次微分方程的解的性質
線性齊次微分方程的解構成了一個向量空間,稱為解空間
考慮一個線性齊次微分方程:
$$
a_n(x) y^{(n)}(x) + a_{n-1}(x) y^{(n-1)}(x) + \cdots + a_1(x) y'(x) + a_0(x) y = 0
$$
- 封閉性:如果 $y_1(x)$ 和 $y_2(x)$ 是這個方程的解,則它們的任何線性組合 $c_1 y_1(x) + c_2 y_2(x)$,其中 $c_1$ 和 $c_2$ 是常數,也是方程的解。這是因為微分算子是線性的,即:
$$
L(c_1 y_1 + c_2 y_2) = c_1 L(y_1) + c_2 L(y_2) = c_1 \cdot 0 + c_2 \cdot 0 = 0
$$
- 加法和純量乘法的相容性:解集中的元素遵循向量加法和純量乘法的規則,因為這些運算是在函數空間中定義的,該空間本身滿足向量空間的所有要求。
由於這些性質,線性齊次微分方程的解構成了一個向量空間,稱為解空間。這個解空間的維度等於微分方程的階數,這意味著如果方程是 $n$ 階的,則存在 $n$ 個線性獨立的解,這些解可以作為解空間的基底。
2. 特解(Particular Solution)
特解是指滿足原始非齊次方程的具體解,這不一定屬於齊次解的解集。求得特解的方法包括但不限於變數係數法、待定係數法。選取特解的形式通常取決於非齊次項 $g(x)$ 的性質,比如多項式、指數函數或三角函數。
3. 一般解(General Solution)
一般解是非齊次線性微分方程的解的最一般形式,它由相應齊次方程的通解和非齊次方程的任何特解組合而成:
$$y(x) = y_h(x) + y_p(x)$$
其中 $y_h(x)$ 是齊次方程的通解,而 $y_p(x)$ 是適當選取的特解,用以滿足非齊次條件。
完整解析實際應用示例:彈簧質塊系統
考慮一個物理系統,其中一個質量為 $m$ 的質塊附著於具有彈簧常數 $k$ 的彈簧,並受到阻尼係數為 $c$ 的阻尼器的影響。此外,質塊受到一個外部力 $F(t) = F_0 \cos(\omega t)$ 的作用。這個系統的運動可以由下列非齊次線性微分方程描述:
$$m \ddot{y}(t) + c \dot{y}(t) + k y(t) = F_0 \cos(\omega t)$$
我們將透過以下步驟來解這個方程:
1. 找出相應的齊次解 $y_h(t)$
對應的齊次方程是:
$$
m \ddot{y}(t) + c \dot{y}(t) + k y(t) = 0
$$
這是一個二階常係數線性齊次微分方程。假設解為 $y(t) = e^{rt}$,代入齊次方程,我們得到特徵方程:
$$
m r^2 + c r + k = 0
$$
解這個二次方程,得到:
$$
r = \frac{-c \pm \sqrt{c^2 – 4mk}}{2m}
$$
這裡,解的形式取決於判別式 $\Delta = c^2 – 4mk$:
- 如果 $\Delta > 0$,兩個實根,解為過阻尼。
- 如果 $\Delta = 0$,一個重根,解為臨界阻尼。
- 如果 $\Delta < 0$,兩個複數根,解為欠阻尼。
假設系統是欠阻尼(最常見的物理情況),則 $r$ 有兩個複數根,形式為:
$$
r = \alpha \pm i \beta
$$
其中:
$$
\alpha = -\frac{c}{2m}
$$
$$
\beta = \frac{\sqrt{4mk – c^2}}{2m}
$$
因此,齊次解 $y_h(t)$ 為:
$$
y_h(t) = e^{\alpha t} \left( A \cos(\beta t) + B \sin(\beta t) \right)
$$
這裡,$e^{\alpha t}$ 是指數衰減項,$\cos(\beta t)$ 和 $\sin(\beta t)$ 是振盪項。這兩部分組成的解是線性獨立的,因為 $\cos(\beta t)$ 和 $\sin(\beta t)$ 是不同的基底函數。
2. 找出特解 $y_p(t)$
我們可以使用待定係數法來尋找特解。假設特解的形式與外力相同:
$$y_p(t) = D \cos(\omega t) + E \sin(\omega t)$$
代入非齊次方程並設定係數等於 $F_0$ 的相對應係數,我們解出 $D = \frac{F_0 k}{k – m \omega^2}$ 和 $E = \frac{F_0 c \omega}{k – m \omega^2}$。
3. 組合解得到一般解
最終的一般解為:
$$y(t) = y_h(t) + y_p(t)$$
這裡的 $y_h(t)$ 和 $y_p(t)$ 分別是從步驟1和步驟2得到的解。
這個例子不僅展示了如何處理典型的工程問題,而且說明了微分方程在實際應用中的直接作用。這種分析對於設計有關動力學系統的工程師來說,是解決問題的基本工具。