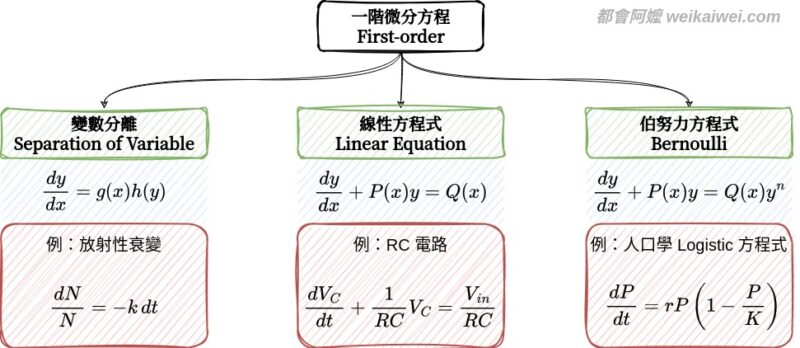
一階微分方程是描述變量之間關係的基本工具,根據方程式的形式,我們可以使用不同的方法來求解。本文將介紹三種常見的一階微分方程求解方法,並給出每種方法的具體例子。教科書裡面通常還有其他種解一階微分方程式的方法,但是那些你通常看過就忘了,這篇文章舉些希望讓你有印象的例子,內化到腦袋裡面,一輩子都有用,對吧!
一、變數分離法(Separable Variables)
方程式形式:
$$\frac{dy}{dx} = g(x)h(y)$$
方法步驟:
- 分離變數:將 $y$ 的函數移到一邊,$x$ 的函數移到另一邊。
- 對兩邊積分。
- 解出 $y$ 作為 $x$ 的函數。
物理例子:放射性衰變 ☢️☢️☢️

在放射性衰變(radioactive decay)中,核素 (nuclides) $N$ 的衰變速率 $\frac{dN}{dt}$ 與當前核素數量 $N$ 成正比關係(核素越多衰變越快)。比例常數 $k$ 稱為衰變常數(decay constant),表示每單位時間內衰變的核素比例。
$$\frac{dN}{dt} = -kN$$
解法:
- 分離變數:
$$\frac{dN}{N} = -k \, dt$$ - 對兩邊積分:
$$\int \frac{1}{N} \, dN = \int -k \, dt$$
$$\ln |N| = -kt + C$$ - 指數化:
$$N = e^{-kt + C}$$
$$N = Ae^{-kt}$$
其中,$A = e^C$ 是積分常數,通常由初始條件 $N(0)$ 確定。
核素的半衰期(half-life),即核素數量減少到其初始值一半所需的時間,是衰變常數的一個重要函數,其公式為:
$$ t_{1/2} = \frac{\ln 2}{k} $$
二、線性微分方程(Linear Differential Equation)
方程式形式:
$$\frac{dy}{dx} + P(x)y = Q(x)$$
方法步驟:
- 計算積分因子 $\mu(x) = e^{\int P(x) dx}$。
- 將方程兩邊乘以積分因子,將其轉換為可積形式。
- 解出 $y$ 作為 $x$ 的函數。
物理例子:RC電路的充電過程 ⚡⚡⚡


RC電路(Resistor-Capacitor Circuit)是由一個 電阻器(Resistor) 和一個 電容器(Capacitor) 組成的簡單電路。這類電路在電子學中極為常見,它們的行為可以用一階線性微分方程來描述,尤其在分析電容器的充電和放電過程中非常有用。
$$\frac{dV_C}{dt} + \frac{1}{RC}V_C = \frac{V_{in}}{RC}$$
解法:
- 計算積分因子 $\mu(t)$:
$$\mu(t) = e^{\int \frac{1}{RC} \, dt} = e^{\frac{t}{RC}}$$ - 乘以積分因子:
$$e^{\frac{t}{RC}} \frac{dV_C}{dt} + \frac{1}{RC} e^{\frac{t}{RC}} V_C = \frac{V_{in}}{RC} e^{\frac{t}{RC}}$$
$$\frac{d}{dt}\left(e^{\frac{t}{RC}} V_C \right) = \frac{V_{in}}{RC} e^{\frac{t}{RC}}$$ - 對兩邊積分:
$$e^{\frac{t}{RC}} V_C = \int \frac{V_{in}}{RC} e^{\frac{t}{RC}} \, dt$$
$$e^{\frac{t}{RC}} V_C = V_{in} e^{\frac{t}{RC}} + C$$
$$V_C = V_{in} + Ce^{-\frac{t}{RC}}$$
在這個表達式中,常數 $C$ 應該通過初始條件確定,比如 $V_C(0)$。如果 $V_C(0) = 0$(電容器初時刻未帶電),則 $C = -V_{in}$:
$$ V_C = V_{in} (1 – e^{-\frac{t}{RC}}) $$
這個方程描述了從電壓為零開始到達到近似 $V_{in}$ 的過程。當 $t \rightarrow \infty$ 時,$V_C(t) \rightarrow V_{in}$。具體來說,當一個 RC 電路開始充電時,電容電壓從零開始逐漸增加,遵循一個指數增長的路徑,直到接近輸入電壓 $V_{in}$。這個過程的物理意義在於它描述了電容器如何儲存能量以及電阻如何限制充電速率。
三、Bernoulli 方程式(Bernoulli Equation)
方程式形式:
$$\frac{dy}{dx} + P(x)y = Q(x)y^n$$
其中,$n \neq 0, 1$。
方法步驟:
- 進行變量變換 $u = y^{1-n}$,將 Bernoulli 方程轉化為線性方程。
- 解相應的線性方程。
物理例子:物種的有限增長 🌱🌱🌱

在生態學和人口動力學中,對於有界限的物種增長模型中最著名的一個是 logistic equation ,這個模型可以用來描述物種在有限資源限制下的增長行為。
$$\frac{dP}{dt} = rP\left(1 – \frac{P}{K}\right)$$
其中,$P$ 是物種的個體數,$r$ 是最大生長率,$K$ 是環境的承載力,即物種個體數量能達到的最大值。
這個方程可以重寫為 Bernoulli 方程的形式:
$$\frac{dP}{dt} – rP = -\frac{r}{K}P^2$$
解法:
- 進行變量變換 $u = P^{-1}$(因為 $n = 2$):
$$u = \frac{1}{P}$$
$$\frac{du}{dt} = -\frac{1}{P^2}\frac{dP}{dt}$$ - 代入原方程式並重新排列:
$$\frac{du}{dt} + ru = r/K$$ - 重新排列得到線性方程:
$$\frac{du}{dt} + ru = \frac{r}{K}$$ - 解線性方程:
- 計算積分因子:
$$\mu(t) = e^{\int r \, dt} = e^{rt}$$ - 乘以積分因子並積分:
$$e^{rt} u = \int \frac{r}{K} e^{rt} \, dt = \frac{1}{K} e^{rt} + C$$ - 代回 $u$ 得到 $P$ 的解:
$$u = \frac{1}{K} + Ce^{-rt}$$
$$P = \frac{1}{u} = \frac{1}{\frac{1}{K} + Ce^{-rt}}$$
$$P = \frac{K}{1 + (\frac{K-P_0}{P_0})e^{-rt}}$$
其中,$P_0$ 是初始種群數量。當 $t = 0$ 時,$P(0) = P_0$。
Logistic Model 描述了在環境資源有限的情況下物種的增長。隨著物種個體數接近環境的承載力$K$,增長速率逐漸減慢,最終穩定在$K$。這個模型非常重要,因為它考慮了環境資源的限制,更符合自然界中物種增長的實際情況。它廣泛應用於生態學、生物學和社會科學中,用於研究人口、細菌或動物的增長和管理。
這樣的解釋和數學描述不僅提供了對生物種群動態的深入了解,還有助於制定有效的管理和保護策略,以確保生物多樣性和生態系統的健康與穩定。
總結
一階微分方程有多種求解方法,選擇正確的方法取決於方程的具體形式。本文介紹了變數分離法、線性微分方程法和 Bernoulli 方程式,每種方法都有其特定的應用情境和求解步驟。希望這些解法能幫助你更好地理解和應用這些求解方法。