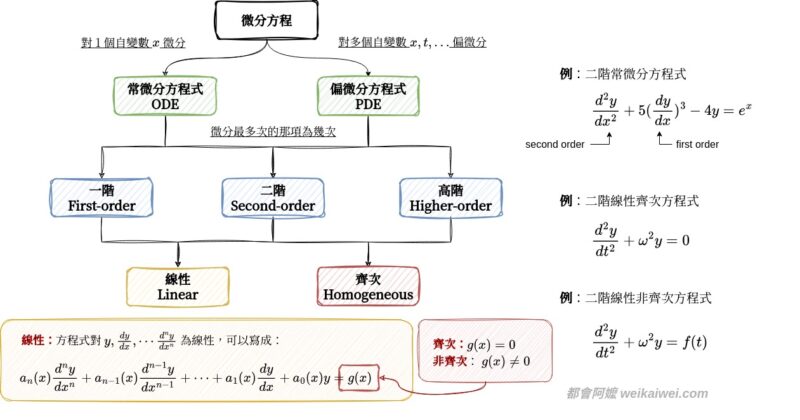
分類微分方程時,心中要有 Type(類型), Order(階數), Linearity(線性性), Homogeneity(齊次性)這四個概念。其中,Order 指的是微分方程中最高階導數的階數,而不是冪次(power)。以下將詳細介紹微分方程的幾種主要分類方式,並給出簡單易懂的解釋。
一、類型 Type (ODE or PDE)
- 常微分方程(Ordinary Differential Equation, ODE):
- 常微分方程只含有一個自變數,例如時間 $t$ 或空間變量 $x$。例子:
$$ \frac{dy}{dx} = ky $$
這個方程表示因變數 $y$ 的變化率與其自身成正比。常微分方程常用於描述單一變量隨時間或空間的變化。
- 偏微分方程(Partial Differential Equation, PDE):
- 偏微分方程含有多個自變數,涉及多個方向上的變化。例如:
$$ \frac{\partial^2 u}{\partial t^2} – c^2 \frac{\partial^2 u}{\partial x^2} = 0 $$
這是波動方程,描述波在介質中的傳播。
二、階數 (Order)
微分方程可以根據最高導數的階數進行分類:
- 一階微分方程(First Order Differential Equation):
- 這類方程只包含一次導數,即 $\frac{dy}{dx}$。例如:
$$ \frac{dy}{dx} = ky $$
這個方程表示因變數 $y$ 的變化率與其自身成正比。
- 二階微分方程(Second Order Differential Equation):
- 這類方程包含二次導數,即 $\frac{d^2y}{dx^2}$。例如:
$$ \frac{d^2y}{dx^2} + 5\frac{dy}{dx} – 4y = e^x $$
這個方程表示因變數 $y$ 的變化受其一次導數和二次導數的影響。
- 高階微分方程(Higher Order Differential Equation):
- 包含三次或更高次數導數的方程。例如:
$$ \frac{d^3y}{dx^3} + 3\frac{d^2y}{dx^2} – 2\frac{dy}{dx} + y = 0 $$
三、線性 (Linearity)
- 線性微分方程(Linear Differential Equation):
- 如果微分方程中所有出現的因變數及其導數都是線性的,即沒有出現平方或其他非線性項,則該方程為線性微分方程。線性微分方程的一般形式為:
$$a_n(x) \frac{d^n y}{dx^n} + a_{n-1}(x) \frac{d^{n-1} y}{dx^{n-1}} + \cdots + a_1(x) \frac{dy}{dx} + a_0(x) y = g(x)$$
這裡,因變數 $y$ 及其各階導數均以線性形式出現,係數 $a_n(x), a_{n-1}(x), \cdots, a_0(x)$ 可以是自變數 $x$ 的函數。例如:
$$ \frac{d^2y}{dt^2} + \omega^2 y = 0 $$
這是一個二階線性微分方程,常見於描述簡諧運動。
- 非線性微分方程(Nonlinear Differential Equation):
- 如果微分方程中存在因變數或其導數的非線性項,則該方程為非線性微分方程。例如:
$$ \left(\frac{dy}{dx}\right)^2 + y^2 = x $$
這類方程通常更難解,但更能真實地描述複雜系統。
四、齊次性 (Homogeneity)
- 齊次微分方程(Homogeneous Differential Equation):
- 齊次微分方程是指方程中所有項均含有因變數 $y$ 或其導數,且方程右側為零。齊次微分方程的一般形式為:
$$a_n(x) \frac{d^n y}{dx^n} + a_{n-1}(x) \frac{d^{n-1} y}{dx^{n-1}} + \cdots + a_1(x) \frac{dy}{dx} + a_0(x) y = 0$$
例子:
$$ \frac{d^2y}{dt^2} + \omega^2 y = 0 $$
這是一個齊次二階微分方程,通常用於描述振動和波動問題。
- 非齊次微分方程(Nonhomogeneous Differential Equation):
- 非齊次微分方程是指方程中存在一個非零的獨立項,即方程右側不為零。非齊次微分方程的一般形式為:
$$a_n(x) \frac{d^n y}{dx^n} + a_{n-1}(x) \frac{d^{n-1} y}{dx^{n-1}} + \cdots + a_1(x) \frac{dy}{dx} + a_0(x) y = g(x)$$
例子:
$$ \frac{d^2y}{dt^2} + \omega^2 y = f(t) $$
在這個方程中,$f(t)$ 是一個非零的獨立項,描述了外力或外部影響下的系統。非齊次微分方程通常用來描述在外部影響下系統的行為。