微分方程 Part4 兩個必懂的微分方程型態振動型、指數型

觀看次數： 984

在學習微分方程的過程中，有一些方程式是非常基礎而重要的。這些方程不僅加深了我們對數學核心理論的理解，而且在物理和工程領域中也有廣泛的應用。本文將介紹兩類關鍵的微分方程：其解涉及振動和指數成長或衰減行為的二階常係數線性齊次微分方程。

這兩個方程式在學習微分方程的時候會不斷遇到！不斷遇到！不斷遇到！不斷遇到！不斷遇到！不斷遇到！不斷遇到！不斷遇到！不斷遇到！

因此直接把這兩個微分方程印在腦海裡，在腦袋內建一個型態辨識的系統，絕對有幫助。

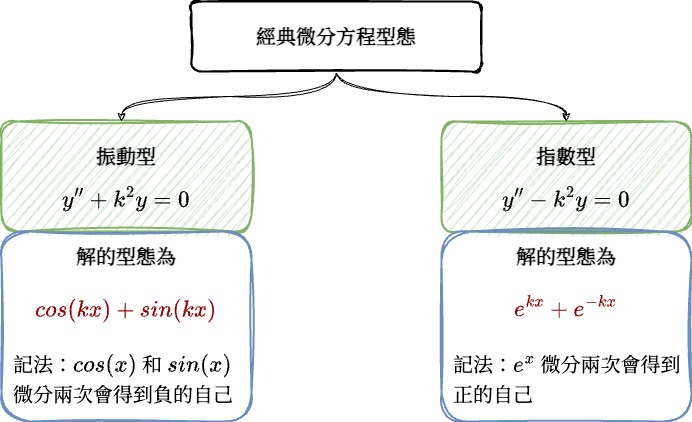
(1) $y” + k^2y = 0$ （振動型）解通常由 $\sin$ 和 $\cos$ 函數疊加而成。
(2) $y” – k^2y = 0$ （指數型）解會由指數函數 $e$ 疊加而成。

心法

怎麼背呢？常常會看到書上或任何筆記裡，看到這種東西直接就把一拖拉庫的 $\sin$ , $\cos$ , $e$ , $\sinh$ , $\cosh$ 砸到你臉上，莫名其妙！但其實可以很間單就識別出這個模式：

1. 對於方程式 $y” + k^2y = 0$ ，也就是 $y” = -k^2y$ ，代表一個方程式微分兩次會變得跟加負號的自己很像。沒錯！ $\sin$ 和 $\cos$ 就是這類函數：

2. 對於方程式 $y” – k^2y = 0$ ，也就是 $y” = k^2y$ ，代表一個方程式微分兩次後會變得跟自己長得很像。沒錯！指數函數 $e$ 正好符合這一特性：

透過這些簡單的規則，我們可以迅速且有效地確認特定微分方程的解的形式，進而深入理解方程的物理意義及其在各種應用中的作用。

讓我們詳細探討這兩種類型的方程及其解的形式，並引入特徵方程式來深化對其解的理解。

考慮二階常係數線性齊次微分方程：
$y” + k^2y = 0$

這是描述簡諧運動的典型方程，其中 $k$ 是系統特性的一個參數，例如彈簧的勁度係數或振動系統的角頻率。為了解這個方程，我們假設解的形式為 $y(t) = e^{rt}$ ，代入方程，得到特徵方程式：
$r^2 + k^2 = 0$

解這個方程，我們得到：
$r = \pm ik$
這意味著解為：
$y(t) = A \cos(kt) + B \sin(kt)$
其中 $A$ 和 $B$ 是由初始條件確定的常數。這種解顯示了系統的振動行為，且振動不衰減。

另一個基本的二階常係數線性齊次微分方程是：
$y” – k^2y = 0$

這種形式的方程涉及指數成長或衰減，解的形式取決於 $k$ 的值。同樣地，我們假設解為 $y(t) = e^{rt}$ ，代入方程導出特徵方程式：
$r^2 – k^2 = 0$

解這個特徵方程，得到：
$r = \pm k$
這產生指數解：
$y(t) = C e^{kt} + D e^{-kt}$
這裡 $C$ 和 $D$ 是由初始條件確定的常數。這類解表示解可能隨時間指數增加或減少，取決於初始條件。

重新組合指數解，我們可以得到：
$y(t) = E \cosh(kt) + F \sinh(kt)$
其中 $E$ 和 $F$ 是新的常數，這表明同一物理現象可以用不同的數學形式來描述。

透過探討振動型和指數型的二階常係數線性齊次微分方程，我們獲得了對這些基礎數學工具的深刻理解。這些方程式不僅在理論上重要，也對解決實際的工程和物理問題至關重要。從理解系統的振動行為到預測指數成長或衰減，這些基礎知識對於設計和控制各種系統都是必不可少的。